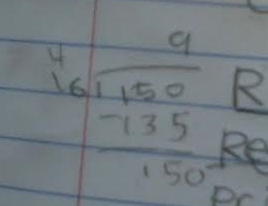We math teachers need to trust each other

I have had a great time working with 5th and 6th graders for two weeks this month. Kids College makes up some of the favorite weeks of my summer. I mean, after all, when a giant trebuchet is involved, it’s hard not to get excited.

But an interesting moment occurred when I looked over a student’s shoulder to see what was in their lab notebook. Here’s what I saw.

See it? It’s significant… You know what? I’ll zoom in.

 

There we go! See that? That is a  straight-up attempt at long division. This might seem mundane and ordinary, but let me tell you why this grabbed my attention.

That student is trying long division. What does that mean?

That means that student was TAUGHT long division by someone. (While acknowledging that this student might be learning long division from a parent, tutor, pastor, or babysitter, I feel like the highest-percentage guess is that the “someone” is a teacher.)

This is important to me because I know several fifth grade teachers who have confirmed that it is common practice for each student to leave elementary school having had the opportunity to learn long division. (I promise, I have a point coming…)

Fast forward that fifth-grader about… mmm… 6 years. Now suppose they are learning this.

Taken from Holt Rinehart Winston’s Algebra II book, 2009 Edition, Page 423

This is, give or take, halfway through Algebra II. Now, I have seen firsthand that this isn’t the easiest skill for a lot of students to master, especially just as it is introduced. In fact, I would go so far as to say that there are plenty of student’s who successfully complete Algebra II while never mastering this particular skill.

There are a lot of reasons that students might not master this skill, one of which might be that THIS is typically the type of situational math problems that this skill gets applied to.

 

Taken from Holt Rinehart Winston’s Algebra II, 2009 Edition, Page 426

But the one that I have heard mentioned to me with the most enthusiasm is that schools are starting to move away from teaching long division. And that division of polynomials is much more difficult to teach to students who haven’t been exposed to long division. Fair enough, except I have a couple of thoughts.

First, (and I’ll admit that this is a little off-topic) even if we assume that the struggling Algebra II students weren’t ever taught long division, what grade do you suspect they should have been? 4th or 5th grade, maybe? It just seems to me that any essential skill that was academically appropriate for 10-year-olds could very well be taught to 17-year-olds. I don’t see any reason to believe that long division is a skill with a window of opportunity to teach that is open to 10-year-olds, but has closed by the time students reach upper adolescence.

However, my second thought is that the evidence I gathered this week confirms what I suspect was true. They WERE taught long division. They fact that they can’t USE long division regularly in their junior year of high school requires a completely separate explanation. There are plenty of potential reasons why, but we shouldn’t allow ourselves to think that the explanation is as simple as “they were never taught that.”

This is a dangerous way to address academic deficiency. This has been a social complaint of schools for a while now. Jay Leno made a regular segment out of it. Every time a clerk has a hard time making change, or a young person appears to struggle balancing his or her checkbook, the question largely becomes “what the heck are they teaching these kids in schools?”

Well, I assure you all, that practically every American middle schooler has been in a math class that has covered the necessary skills to make change or balance a checkbook.

Just like we teach European geography, basic grammar, and the names of the Great Lakes.

But not every student learns it. And whose to blame?

I don’t know, but as a teacher, there aren’t a ton of folks giving me the benefit-of-the-doubt these days. We should, at least, be able to expect it from the person who teaches down the hall, down stairs, or in the building next door.

Common core is trying to deal with the “when to students get taught this” conundrum because there is a lot of social pressure that assumes that the problems with missing knowledge is missing instruction. I’m not sure if Common Core has what it takes to address that issue…

… especially if that isn’t the issue. Because what happens when we make sure that every fifth grader coast-to-coast is taught long division and 6 years later, coast-to-coast, the 17-year-olds are still unfamiliar with it?

“Ugg.. I don’t get ANY of this…”

I like working with teenagers for a lot of reasons. One such reason is because it is usually quite easy to get bold, absolute statements out of them.

For example: “I don’t get ANY of this.” (emphasis not mine…).

It’s tricky business handling that statement because most of the time, the author of that quote genuinely feels that way. That doesn’t make the it true, but if he or she is already feeling like all the attempts at math are turning up wrong, combating their perception by simply saying it’s false is probably not the best approach.

I enter into evidence the following photo:

 

See it? He made the same mistake twice.

I gave these two problems as part of a short formative assessment. I saw the answers shown above a bunch. Most of my classes were lamenting the assessment because, “They don’t get any of this.”

Which, as I said above, couldn’t be farther from the truth. Those two answers show quite a lot of understanding, actually. There is a single mistake that led to incorrect response in both cases. That student was unable to distinguish the shorter leg from the longer leg. That’s it. Fix that and the answers get better.

And when I show them the answer to those two, many of those bold, absolute thinkers are likely going to think, “Yup, I knew it. It’s wrong. I knew I didn’t get any of this.”

At least I know that going into the discussion. Now, if I can just convince them that understanding is a spectrum more than a light switch.

Feeding The Elephant in the Room

I am going to ramble a bit in this piece, but as you read, keep a specific thought in your mind:

When our students have graduated high school, we will know we educators have done our job because _____________________.

Now, onto the ramble:

So, a lot gets said about the struggles of American secondary education. Recently, Dr. Laurence Steinberg took his turn in Slate coming right out in the title and calling high schools “disasters”. Which, as you can imagine, got some responses from the educational community.

Go ahead and give the article a read. I’ll admit that education is not known as the most provocative topic in the American mainstream, but Dr. Steinberg has written a piece that has been shared on Facebook a few thousand times and on twitter a few hundred more. It’s instigated some thoughtful blog responses. You have to respect his formula.

He starts with a nice mini Obama dig.

Makes a nice bold statement early (“American high schools, in particular, are a disaster.”)

Offers a “little-known” study early to establish a little authority.

Then hits the boring note and hits it hard. High school is boring. Lower level students feel like they don’t belong. Advanced students feel unchallenged. American schools is more boring than most other countries’ schools.

Then he goes on to discredit a variety of things education has tried to do over the last 50 (or so) years including: NCLB, Vouchers, Charters, Increased funding, lowering student-to-teacher ratio, lengthening the school day, lengthening the school year, pushing for college-readiness. I mean, with that list, there’s something for everyone

Like it or hate it, that is an article that is going to get read.

However, there isn’t a lot in the way of tangible solutions. The closest Dr. Steinberg comes is in this passage: ” Research on the determinants of success in adolescence and beyond has come to a similar conclusion: If we want our teenagers to thrive, we need to help them develop the non-cognitive traits it takes to complete a college degree—traits like determination, self-control, and grit. This means classes that really challenge students to work hard…”

Nothin’ to it, right? It’s as easy as making our students “grittier”.

Now, I will repeat the introductory thought: When our students have graduated high school, we will know we educators have done our job because _____________________.

That blank gets filled in a variety of ways from the area of employability, or social responsibility, or liberation and freedom, or social justice to a variety of other thises and thats that we use our high schools for. We are using our high schools as the training ground for the elimination of a wide variety of undesirable social things. We’ve used our schools to eliminate obesity, teen pregnancy and STIs, discrimination based on race, gender, or alternative lifestyles. We have allowed colleges to push college-readiness to make their job easier. We’ve allowed employers to push employability to make their jobs easier. The tech industry feels like we need more STEM. There’s a push-back from folks like Sir Ken Robinson who feel like it’s dangerous to disregard the arts.

And they all have valid points. I’m certainly not mocking or belittling any of those ideas.

However, very little is getting said on behalf of the school. We are treating the school as a transparent entity with none of its own roles and responsibilities. It is simply the clay that gets molded into whatever society decides it should be. Well, since the 60’s, society has had a darned hard time making up its mind about what it wants and so the school has become battered and bruised with all the different initiatives and plans, data sets, and reform operations. Reform is an interesting idea when the school hasn’t ever formally been formed in the first place.

So, we have this social institution that we send 100% of our teenagers to in some form or another and we don’t know what the heck its for. No wonder, as Dr. Steinberg puts it, “In America, high school is for socializing. It’s a convenient gathering place, where the really important activities are interrupted by all those annoying classes. For all but the very best American students—the ones in AP classes bound for the nation’s most selective colleges and universities—high school is tedious and unchallenging.”

Public enemy #1 needs to be the utter and complete lack of purpose in the high school system. We are running our young people through exercises… why? For what? What do we hope to have happen at the end? When we decide the answer to that question, then we eliminate the rest. It isn’t lazy to say, “I’m not doing that, because that isn’t my job.” It’s efficient. If you start doing the work of others, you stop doing your work as well.

We’ve never agreed on the work of the American high school, but I suspect some of what we are asking it to do should belong on the shoulders of something or someone else. I suspect as soon as we establish a purpose and simplify the operations around that purpose, we can start to see some progress on the goals that we have for our schools, which will spell success for our students and start to clean up the disaster that so many feel like the high schools currently are.

Perplexing the students… by accident.

It seems like in undergrad, the line sounds kind of like this: “Just pick a nice open-ended question and have the students discuss it.” It sounds really good, too.

Except sometimes the students aren’t in the mood to talk. Or they would rather talk about a different part of the problem than you intended. Or their skill set isn’t strong enough in the right areas to engage the discussion. Or the loudest voice in the room shuts the conversation down. Or… something else happens. It’s a fact of teaching. Open-ended questions don’t always lead to discussions. And even if they did, class discussions aren’t always the yellow-brick road lead to the magical land of learning.

But sometimes they are. Today, it was. And today, it certainly wasn’t from the open-ended question that I was expecting. We are in the early stages of our unit on similarity. I had given a handout that included this picture…

… and I had asked them to pair up the corresponding parts.

The first thing that happened is that half-ish of the students determined that in figures that are connected by a scale factor (we hadn’t defined “similar” yet), each angle in one image has a congruent match in the other image. This is a nice observation. They didn’t flat out say that they had made that assumption, but they behaved as though they did and I suspect it is because angles are easier to measure on a larger image. So, being high school students and wanted to save a bit of time, they measured the angles in the bigger quadrilateral and then simply filled in the matching angles in the other.

Here’s were the fun begins. You see, each quadrilateral has two acute angles. Those angles have measures that are NOT that different (depending on the person wielding the protractor, maybe only 10 degrees difference). And it worked perfectly that about half of the class paired up one set of angles and the other half disagreed. And they both cared that they were right. It was the perfect storm!

Not wanting to remeasure, they ran through all sorts of different explanations to how they were right, which led us to eventually try labeling side lengths to try to sides to identify included angles for the sake of matching up corresponding sides. But, that line of thought wasn’t clear to everyone, which offered growth potential there as well.

By the time we came to an agreement on where the angle measures go, the class pretty much agreed that:

1. Matching corresponding parts in similar polygons is not nearly as easy as it is in congruent polygons.

2. Similar polygons have congruent corresponding angles.

3. The longest side in the big shape will correspond to the longest side in the small shape. The second longest side in the big, will correspond to the second longest side in the small. The third… and so on.

4. Corresponding angles will be “located” in the same spot relative to the side lengths. For example, the angle included by the longest side and the second longest side in the big polygon will correspond to the angle included by the longest side and the second longest side in the small polygon. (This was a tricky idea for a few of them, but they were trying to get it.)

5. Not knowing which polygon is a “pre-image” (so to speak) means that we have to be prepared to discuss two different scale factors, which are reciprocals of each other. (To be fair, this is a point that has come up prior to this class discussion, but it settled in for a few of them today.)

I’d say that’s a pretty good set of statements for a class discussion I never saw coming.

Fake-World Math, Real-World Engagement

Dan Meyer is currently leading a very engaging #MTBoS discussion regarding “Real World Math” and it’s effects on student engagement with respect to completing (with quality) mathematical tasks. In general, “real world” is a term describing a task that attempts to emulate a task that might actually happen to someone in a non-school setting. The prevailing thought in many circles is that as a mathematical task becomes more “real world” it will become more engaging to students.

Many of us have plenty of anecdotal evidence to challenge that generalization.

Enter the “fake world” math tasks.

“Fake World” is a term used by Meyer to describe mathematical tasks that are engaging to students and encourage/require authentic mathematical problem-solving, but doesn’t attempt to emulate any actual action or task that one might use in a non-school setting. The Magic Octagon is an excellent example of a “fake-world” task. This is not a task that would EVER be asked of you in your family, work, or spiritual lives outside of school, but it is worth 20 good minutes of almost 100% engagement in a geometry classroom. These types of experiences cast doubt on the presupposed direct relationship between “real world” and student engagement.

As part of this, Mr. Meyer is attempting to do a bit of data collection to get a sense of what fake-world math activities we find engaging in our free time.

For me, it’s Flow Free on my iPad. I’ve seen this wonderful little logic game draw in 31-year-olds (my wife and I), high school kids (in my classes), and my 4-year-old daughter can get lost on it for an hour straight if I’d let her.

The task of a game is fairly simple. There are exactly two dots of each color on a grid. The goal is to connect each dot to its corresponding dot with a path that doesn’t intersect any other path. Also, each square on the grid needs to have a path going through it. No empty boxes.

So one solution to the above board would look like this:

At this point, you can either try again to complete the same puzzle in fewer moves or move on to the next puzzle. As you might expect, the puzzles get progressively more difficult with additional colors added and the grids increasing from 5 X 5 to 6 x 6 and 7 x 7.

But what is it about this game that is so engaging?

The simplicity of the goal is a start. It takes very little explanation to begin playing. Also, the first couple of puzzles are quite easy to allow you to get the hang of the game.

The progressively more difficult puzzles is helpful as well. As you play, you start to develop some strategies and thought processes that you want to take for a spin on some harder puzzles. This game makes sure you get that chance.

Also, I like that the game has unlimited do-overs. If I had to do some guessing-and-checking to complete a puzzle and I want to start it over again, I can do that an unlimited number of times until I am happy enough to move on. Or I can move on right away.

It seems like those qualities could be integrated into math class. Consider an activity with a low entry point, a simple goal, some do-overs offered, and additional pieces that make the problem more difficult once the easier “levels” are solved. That would require us who design activities to take a more inductive approach to building engagement models. Look at what is engaging and see what elements they have in common.

I would absolutely encourage everyone to get involved in Mr. Meyer’s conversation. Do you have a “fake-world” math activity that you find engaging? Head over and tell the MTBoS about it in the comments.