Dan Meyer is currently leading a very engaging #MTBoS discussion regarding “Real World Math” and it’s effects on student engagement with respect to completing (with quality) mathematical tasks. In general, “real world” is a term describing a task that attempts to emulate a task that might actually happen to someone in a non-school setting. The prevailing thought in many circles is that as a mathematical task becomes more “real world” it will become more engaging to students.
Many of us have plenty of anecdotal evidence to challenge that generalization.
Enter the “fake world” math tasks.
“Fake World” is a term used by Meyer to describe mathematical tasks that are engaging to students and encourage/require authentic mathematical problem-solving, but doesn’t attempt to emulate any actual action or task that one might use in a non-school setting. The Magic Octagon is an excellent example of a “fake-world” task. This is not a task that would EVER be asked of you in your family, work, or spiritual lives outside of school, but it is worth 20 good minutes of almost 100% engagement in a geometry classroom. These types of experiences cast doubt on the presupposed direct relationship between “real world” and student engagement.
As part of this, Mr. Meyer is attempting to do a bit of data collection to get a sense of what fake-world math activities we find engaging in our free time.
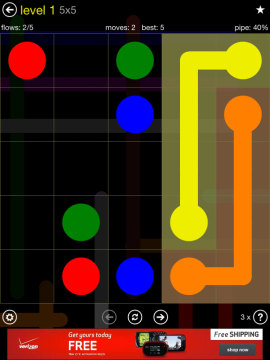
For me, it’s Flow Free on my iPad. I’ve seen this wonderful little logic game draw in 31-year-olds (my wife and I), high school kids (in my classes), and my 4-year-old daughter can get lost on it for an hour straight if I’d let her.
The task of a game is fairly simple. There are exactly two dots of each color on a grid. The goal is to connect each dot to its corresponding dot with a path that doesn’t intersect any other path. Also, each square on the grid needs to have a path going through it. No empty boxes.
So one solution to the above board would look like this:
At this point, you can either try again to complete the same puzzle in fewer moves or move on to the next puzzle. As you might expect, the puzzles get progressively more difficult with additional colors added and the grids increasing from 5 X 5 to 6 x 6 and 7 x 7.
But what is it about this game that is so engaging?
The simplicity of the goal is a start. It takes very little explanation to begin playing. Also, the first couple of puzzles are quite easy to allow you to get the hang of the game.
The progressively more difficult puzzles is helpful as well. As you play, you start to develop some strategies and thought processes that you want to take for a spin on some harder puzzles. This game makes sure you get that chance.
Also, I like that the game has unlimited do-overs. If I had to do some guessing-and-checking to complete a puzzle and I want to start it over again, I can do that an unlimited number of times until I am happy enough to move on. Or I can move on right away.
It seems like those qualities could be integrated into math class. Consider an activity with a low entry point, a simple goal, some do-overs offered, and additional pieces that make the problem more difficult once the easier “levels” are solved. That would require us who design activities to take a more inductive approach to building engagement models. Look at what is engaging and see what elements they have in common.
I would absolutely encourage everyone to get involved in Mr. Meyer’s conversation. Do you have a “fake-world” math activity that you find engaging? Head over and tell the MTBoS about it in the comments.